What is a sample in research: Definition, examples & tips

Researchers can conduct studies on large populations. It is highly unusual for researchers to be able to get information from every member of a group of individuals they are studying. If you are researching a large population, you can pick a sample. 

The population that will participate in the study is the sample. Using samples, researchers may perform their experiments more quickly and with more manageable data. This article will explain the definition of a sample in research, what a sample is in statistics with examples, how researchers choose a sample, and how to determine the correct sample size for your research with all details.

What is a sample?

A sample is a condensed, controllable representation of a larger group. It is a subgroup of people with traits from a wider population. When the population size is too large for the test to include all potential participants or observations, samples are utilized in statistical testing. 

The definition of a sample

A sample is an analytical subset of a larger population in statistics. The sample should be representative of the population as a whole and should not show bias toward any particular characteristic. The researcher gains knowledge from the sample that can be applied to the entire population.  

How do researchers choose a sample?

Sampling is an essential component of the research design as it gathers information that can be used in a research study. Probability sampling and non probability sampling are the essential methodologies that define sampling techniques. 

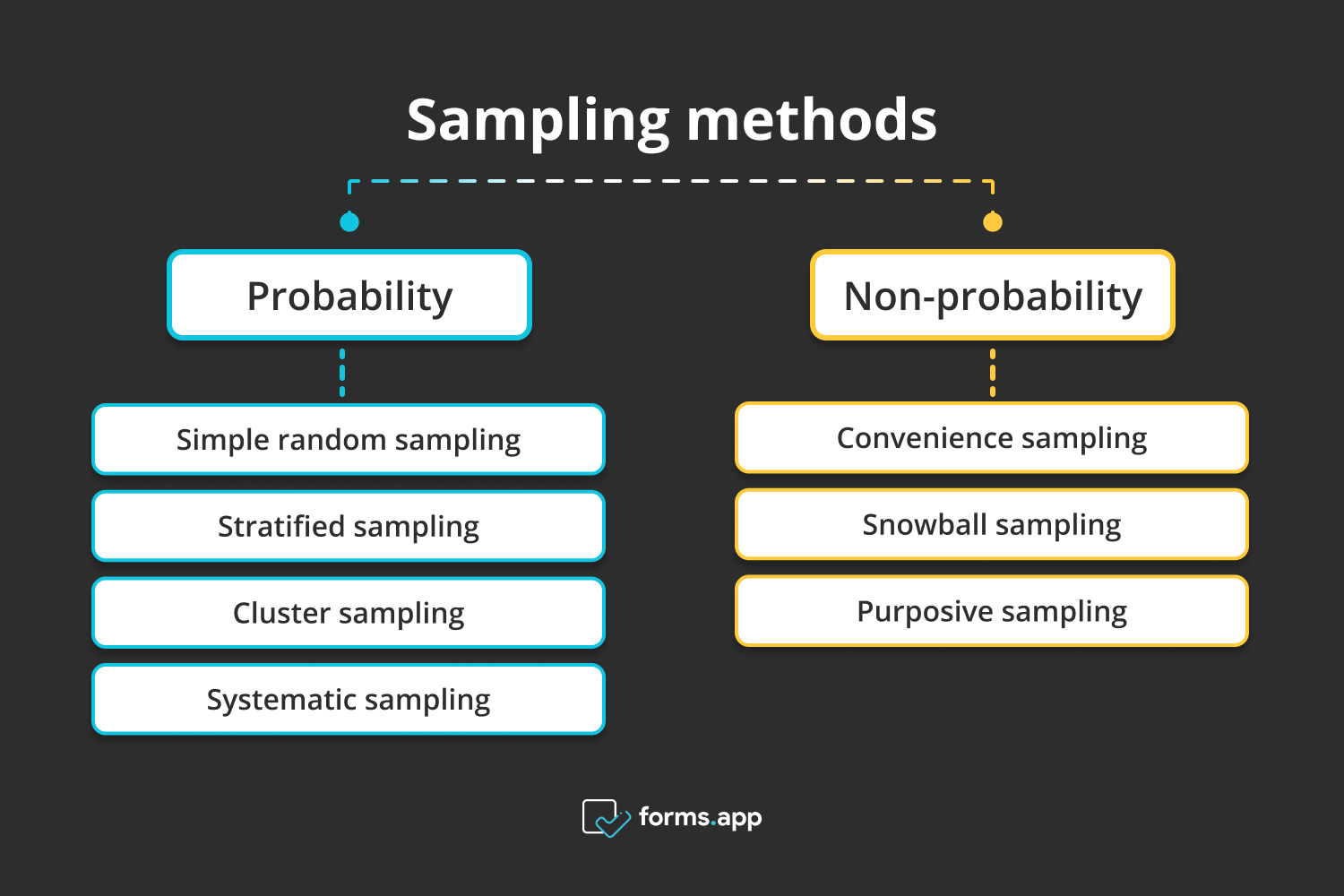
Sampling methodologies

Probability sampling

Probability sampling is a sampling technique that entails randomly picking a sample or a section of the population. It is also known as random sampling. When procedures are established to guarantee that each unit within a population has an equal probability of being picked, this is known as random selection.  Here are 4 types of probability sampling designs that are frequently used. 

1 - Simple random sampling

Simple random sampling takes a random selection from the whole population with an equal probability of selection for each unit. The most typical method of choosing a random sample is the one. 

Consider creating a list of every person in the population and giving them a number. Using a random number table, random number table, or random number generator, you choose samples at random from this population. 

2 - Stratified sampling

Stratified sampling randomly chooses a sample from one or more strata or population subgroups. Each group is distinguished from the others based on a shared trait, such as age, gender, color, and religion. 

By doing this, you can ensure that your sample population sufficiently represents each subgroup of a particular community. For example, if you divide a student population by university majors, Architecture, Linguistics, and Teaching departments, students are three different tiers within that population. 

3 - Cluster sampling

The cluster sampling method divides the population into clusters, which are smaller groupings. Then, you choose a sample of people at random from these clusters. Large or geographically distributed populations are frequently studied using cluster sampling. 

For example, you may divide all cities into neighborhoods or clusters and then choose the areas with the most significant population while filtering by mobile device users to see how well your goods perform across a city.

4 - Systematic sampling

When using systematic sampling, units are chosen at regular intervals beginning at a random point, drawing a random sample from the target population. Every member of the population is assigned a number in systematic sampling,  but rather than being a random selection procedure, people are picked out at predetermined intervals. 

For example, while 1000 vaccine volunteers are selected from a list of 5000 applicants, each applicant is given a number from 1 to 5000. A sample of 1000 volunteers can then be obtained by starting at 1 and selecting each participant on 10 to an item scale.

Nonprobability sampling

When the number of units in the population is either unknown or difficult to identify individuals, nonprobability sampling approaches are utilized in quantitative and qualitative research. Additionally, it is employed when you wish to limit the results’ applicability to a particular group or organization rather than the broader populace. 

Besides the advantages of non-probability sampling, the most significant disadvantage is the possibility of sampling bias. As the sample selection process unfairly favors some population members over others. Here are some types of nonprobability sampling:

1. Convenience sampling

Convenience sampling comprises those who are easiest to research by the researcher. Researchers selected these samples only because they are simple to compile, and they did not think to choose a sample representative of the total population. 

For example, researchers conducted a shopping mall response survey to understand a product manufacturer's likelihood of customers using the products. In this sampling method, sample participants are selected based on their proximity to the survey table and their willingness to participate in the research.  

2. Snowball sampling

Snowball sampling is used to recruit participants through other participants if the population is difficult to reach. As you interact with additional individuals, your network of contacts "snowballs" in size.

For example, you are looking into local homeless people's experiences. Since there is no list of every homeless person in the city, probability sampling is not an option. One of the persons you meet agrees to participate in the research, and the homeless person refers you to other local homeless people he knows.

3. Purposive sampling

Purposive sampling is frequently employed in qualitative research when the researcher prefers to learn in-depth information about a particular phenomenon versus drawing general conclusions from statistics or when the population is relatively tiny and focused.

For instance, a researcher wants to learn more about how people with persistent headaches live. In such instances, they can choose a sample of people diagnosed with persistent headaches using purposive sampling. 

How to determine the right sample size

The sample size is crucial for reliable, statistically meaningful results and a smooth research operation. You should learn the fundamentals of the statistics involved to select the appropriate sample size, considering a few distinct elements that may affect your study.

1. Population size

The population size is the total number of individuals that can be included in the study. To determine the appropriate population size, you should be clear about who belongs or doesn’t belong in your group. 

2. The margin of error (confidence interval)

Errors are inevitable in research studies. The margin of error is represented by a percentage, which is a statistical inference about the confidence that the number of respondents accurately represents the opinions of the whole population.  

3. Confidence level

The confidence level value measures your degree of certainty on how closely a sample reflects the total population within your chosen margin of error. The most prevalent are the 90%, 95%, and 99% confidence intervals.

4. Standard deviation

The standard deviation indicates how much variation you can expect in your responses. A safe value to use as a guide is 0.5, which denotes that significant sample size is required.

Sample size formula

You may select the appropriate sample size by considering various factors affecting your study. You may compute the sample using an online calculator or read on to learn how to do it by hand.

1. Discover the Z-score

The Z-score displays how far a certain ratio deviates from the mean by standard deviation. You should translate your degree of confidence into a Z-score.

For the most typical confidence levels, the Z-scores are as follows:

2. Apply the formula for the sample size

Use the following formula to perform the calculation manually. 

Sample size formula

Frequently asked questions about sample

A sample is a particular group from which you will gather data. You should employ a sample when your population is sizable, spread geographically, or challenging. The population, sample, and sample frame are different from each other. Here are the frequently asked questions about the sample.

Key points to takeaway

In conclusion, a sample is a group or subset of persons or things chosen from a broader population to study or assess particular traits or behaviors. To guarantee that every member of the population has an equal chance of being chosen, the sample should be representative of the people from which it is collected or selected using a random sampling procedure. 

Selecting the appropriate sample technique based on the research topic, budget, and available resources. Additionally, the accuracy and generalizability of the results are greatly influenced by the sample size. 

This article has explained what a sample is in research methodology, what sample is in research examples, and how to determine the correct sample size. You can learn more about the research by reading this article.