The sample size refers to the number of participants in a sample size in market research. The sample size considers a group of participants chosen from the general population representing the study’s target population.
When determining the target sample size, it is essential to avoid the tendency to choose an unjustifiably small population or the inclination to select an unjustifiably large population. Several factors affect sample size. The foremost of these factors is the research type.
When you determine the sample size, you may consider the research type. This article will explain the correlation between the kind of research and the sample size, the standard sample size, how to determine the correct sample, and the sample size formula in all detail.
Is there a standard sample size for some research studies?
There are resource and statistical considerations when determining sample sizes. When the population is large, 100 participants are typically considered the minimum sample size. However, the proposed data analysis type and the anticipated response rate are influential determinants of the sample size in most studies.
The majority of statisticians agree that a sample size of 100 is necessary to obtain any kind of significant results. If your population is less than 100, you should survey every single person.
You can consider some factors when determining the appropriate sample size, such as research type, confidence level, or standard deviation. The types of research methods have a strong relation to sample size. Before you determine the sample size, you should understand your research type.
Choosing a sample size for a correlational study
The correlational study aims to find the relationship between two or more variables and their causes and effects. Due to the study’s use of numerical data and lack of variable manipulation, it can be said that it falls under the category of nonexperimental quantitative research.
According to Fraenkel Wallen, a correlational study's minimum acceptable sample size is at least 30. Additionally, they state that data from samples smaller than 30 may not reflect the degree of correlation.
Choosing a sample size for a clinical study
A crucial step in planning a clinical study is determining the sample size. The sample size must be carefully planned to avoid wasting money, staff time, and research resources. A study’s inability to identify significant treatment effects due to inadequate sample size is not uncommon. The specified statistical hypotheses and a few study design factors determine an appropriate sample size. These include the desired statistical power, the significance level, the desired statistical power and the minimal meaningful detectable difference (effect size).
Choosing a sample size for studies with repeated measures
Collecting repeated measures can lower study costs while simultaneously boosting statistical power for spotting changes. The correlations between repeated measurements from the same participant must be considered when determining the proper sample size.
How to determine the correct sample size

Factors to consider for the correct sample size
You should understand the statistics and consider several factors affecting your research to select the appropriate sample size. After that, you can use a sample size formula to put everything together and sample with assurance because you will know that there is a good chance your survey is statistically accurate.
The following steps are appropriate to find a sample size for data whose continuous data is counted numerically. You should not apply it to categorical data. Determine a few details about the target population and the required level of accuracy before you can calculate a sample size:
1 - Population size: You should define who belongs and who doesn’t belong in your group to determine the total number of people you refer to. For example, if you research cars and want to learn about car owners, you will include anyone who has owned at least one car at some point. If you cannot calculate the exact number, don’t worry. It is typical to have an undetermined total or an estimated range.
2 - The margin of error: Errors are unavoidable. You can decide how much variance between the means of your sample and the population you want to allow.
3 - Confidence level: Confidence level refers to your assurance that the actual mean will fall within your margin of error. 90%, 95%, and 99% confidence levels are the most typical confidence intervals.
4 - Standard deviation: The formal derivation asks you to predict the degree to which the responses you receive will differ from one another and the mean value.
The values all be grouped around the mean if the standard derivation is low, as opposed to high formal derivation. This indicates that the matter is dispersed over a much more comprehensive range with extremely small and large outlying figures.
Since your survey hasn’t been administered yet, a safe option is a standard derivation of 0.5, which will help ensure that your sample size is adequate.
The sample size formula
The sample size formula uses the distinction between the population and sample to help you determine the appropriate sample size. This sample size is the number of observations within a particular sample population. Since it is impossible to screen the entire population, a sample is taken, and a survey or surveys are conducted.
The sample size formula is calculated in two steps. First, the sample is determined for the entire population, and then the sample size is disturbed among the necessary people. The formula is as follows:
1 - Find the Z-score
The Z-score displays how far a given ratio deviates from the mean by standard deviation. You should convert your level of confidence into a Z-sore. The Z-scores for the most typical confidence levels are listed below:
- 90% Z-score = 1.645
- 95% – Z Score = 1.96
- 99% – Z Score = 2.576

Find the Z-score
2 - Utilize the sample size formula
After calculating your Z-score, standard deviation, and confidence interval for the sample size, you can start using the formula. You can use the following formula to perform the calculation manually:
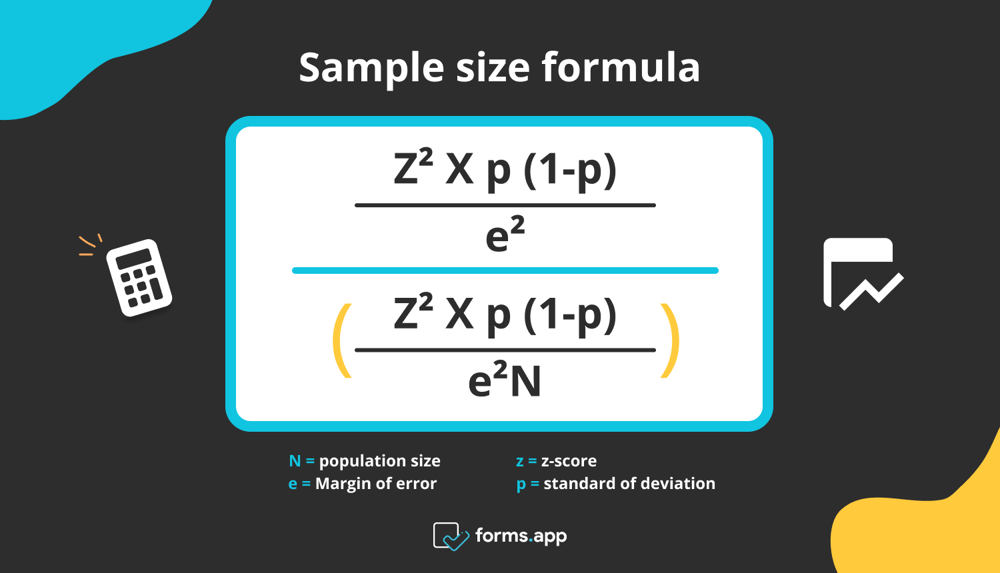
- [z2 X p(1-p)] / e2 / 1 + [z2 X p(1-p)] / e2 X N]
- N = population size
- e = Margin of error
- z = z-score
- p = standard of deviation
Utilize the sample size formula
Conclusion
In conclusion, the sample size is crucial for accurate, statistically significant results and a successful study. The research is more effective when the sample is appropriate because the results are trustworthy, and the use of resources is kept to a minimum while upholding ethical standards. There is a correlation between the research type and sample size. You can consider the research type and other essential factors mentioned above when determining the right sample size.
Sample size calculations directly impact research results. Very small sample sizes compromise a study’s external and internal validity. In contrast, conducting the fundamental research will be difficult, expensive, and time-consuming if the sample is too large. To choose the correct sample size for your research, you should understand the underlying statistics and the research design types and consider several variations.
Contributors
forms.app, your free form builder
- Unlimited views
- Unlimited questions
- Unlimited notifications



