La régression ou la régression simple est une méthode d'analyse largement utilisée par le monde de la finance et les disciplines connexes. Allez-vous investir ? Faites une analyse de régression. Allez-vous examiner les prix des matières premières ? La régression est la solution. Vous pouvez bénéficier de l'analyse de régression lors de prises de décision qui affecteront les finances de votre entreprise.
Dans cet article, une définition simple de l'analyse de régression sera donnée. Les principaux types d'analyse et leurs exemples seront répertoriés. Ses avantages seront présentés afin que vous compreniez pourquoi vous devriez utiliser cette analyse. Alors n'attendez plus et commencez à lire l'article.
Qu'est-ce que l'analyse de régression ?
L'analyse de régression est une méthode de recherche utilisée pour mesurer les liens entre une ou plusieurs variables indépendantes et une variable dépendante.
Elle aide à estimer la valeur d'une variable dépendante en examinant les changements qui se produisent autour d'elle. Cela est généralement objectif car il s'agit de données mathématiques. Elle est utilisée avec la visualisation des données à l'aide d'outils appropriés et révèle des modèles de points de données courbes ou linéaires. Ainsi, les entreprises auront des informations préliminaires sur les situations futures en utilisant cette méthode d'analyse.
Types et exemples d'analyse de régression
Lors de l'analyse des données, vous pouvez utiliser plusieurs méthodologies. Chaque méthodologie contient des calculs uniques et offre des informations efficaces sur différents sujets.
Vous pouvez toujours profiter de différents types de techniques d'analyse de données, telles que l'analyse de cluster et l'analyse conjointe. Cependant, l'analyse de régression sera toujours votre première référence pour la modélisation statistique. Pour l'instant, des exemples d'analyse de régression pour chaque type seront mentionnés ci-dessous:

Types d'analyse de régression
1. Analyse de régression linéaire
La régression linéaire simple est une méthode statistique utilisée pour modéliser la relation entre une seule variable indépendante (prédicteur) et une variable dépendante. Ici, une relation linéaire est supposée. Cela signifie que s'il y a un changement dans la variable prédicteur, il y a une équivalence proportionnelle dans la variable dépendante. Le but de cette méthode est de faire des prédictions sur la variable dépendante. Elle sera également utilisée pour se préparer à des modèles de régression plus complexes.
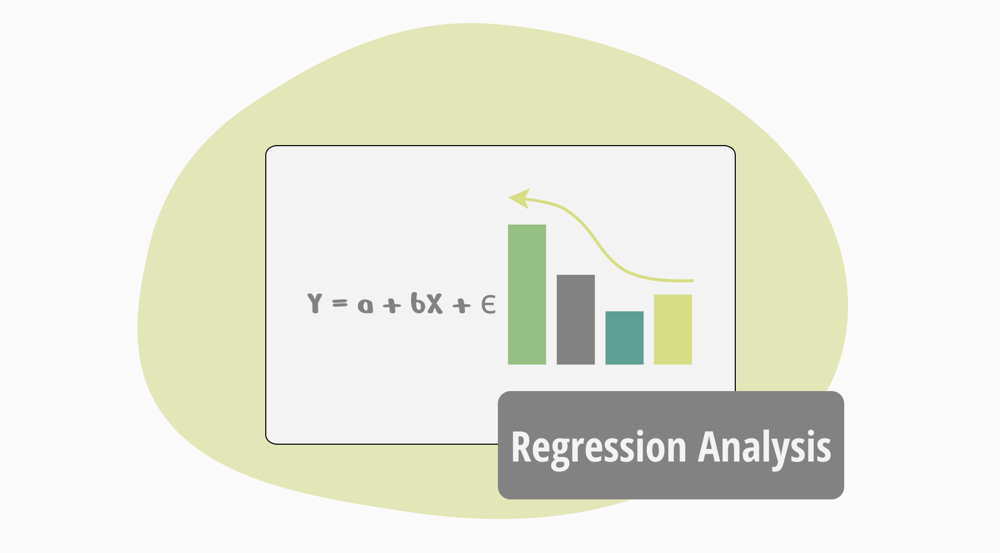
Formule de régression:
Y = a + bX + ϵ
Y – Variable dépendante
X – Variable indépendante
a – Intercept
b – Pente
ϵ – Résidu (erreur)
Exemple: Vous voulez créer un modèle pour trouver le magasin qui convient à votre objectif et estimer les prix des magasins. Disons qu'un prix de magasin spécifique est une variable dépendante. Cela coûte X dollars. La variable indépendante est la surface du bâtiment. Vous analysez la relation entre les deux variables. Avec la ligne de meilleure correspondance, vous rendez les prix des magasins visibles et prévisibles dans la modélisation.
2. Analyse de régression multiple
L'analyse de régression multiple est réalisée en ajoutant plus d'une variable au modèle de régression linéaire simple. Le but ici est de trouver le coefficient de chaque valeur avec une combinaison linéaire. Cela vous permet de comprendre comment les changements simultanés dans différents prédicteurs affectent la variable dépendante.
Exemple: Dans ce type d'analyse, vous ajoutez des caractéristiques au magasin que vous recherchez ci-dessus. Par exemple, il peut avoir une cave, un parking, un grenier, etc. Lorsque des caractéristiques architecturales sont ajoutées, vous observez si les prix des magasins changent.
3. Analyse de régression logistique
Cette méthode est non linéaire et est utilisée pour estimer la probabilité d'événements se produisant avec une ou plusieurs variables. Une variable binaire logique est utilisée ici, c'est-à-dire oui/non, vrai/faux. Les probabilités sont cartographiées sur une fonction appelée courbe sigmoïde. Autrement dit, les combinaisons sont converties en probabilités entre 0 et 1.
Exemple : Vous souhaitez calculer les probabilités que vos clients choisissent votre nouveau produit. Tout d'abord, vous préparez un ensemble de données qui inclut les données démographiques de vos clients et leurs attitudes envers les produits que vous avez précédemment lancés. Avec la modélisation logistique adaptée à ces données, vous pouvez apprendre les résultats possibles sous forme binaire. Vous pouvez également analyser plus en détail le comportement des clients avec l'analyse narrative.
4. Analyse de régression polynomiale
Il s'agit d'une technique de régression utilisée pour modéliser des variables dans une relation non linéaire. Elle offre une analyse de données plus flexible. L'analyse de régression polynomiale est votre source de référence, en particulier lorsque vous réalisez un modèle peu performant et que vous vous rendez compte qu'il ne correspond pas aux valeurs réelles. Elle vous permet de prédire la ligne d'ajustement la plus adaptée en suivant les schémas des points de données.
Exemple : Vous souhaitez analyser si un produit alimentaire se vend davantage en fonction des saisons. Vous collectez des données sur les produits alimentaires que vous vendez en fonction des mois et des saisons. Cependant, il est évident qu'il n'y a pas de relation linéaire, vous appliquez donc une analyse de régression polynomiale. Avec la courbe polynomiale, vous pouvez prédire les fluctuations saisonnières de manière plus précise. Ainsi, l'environnement est préparé pour les stratégies du nouveau marché.
Avantages de l'analyse de régression
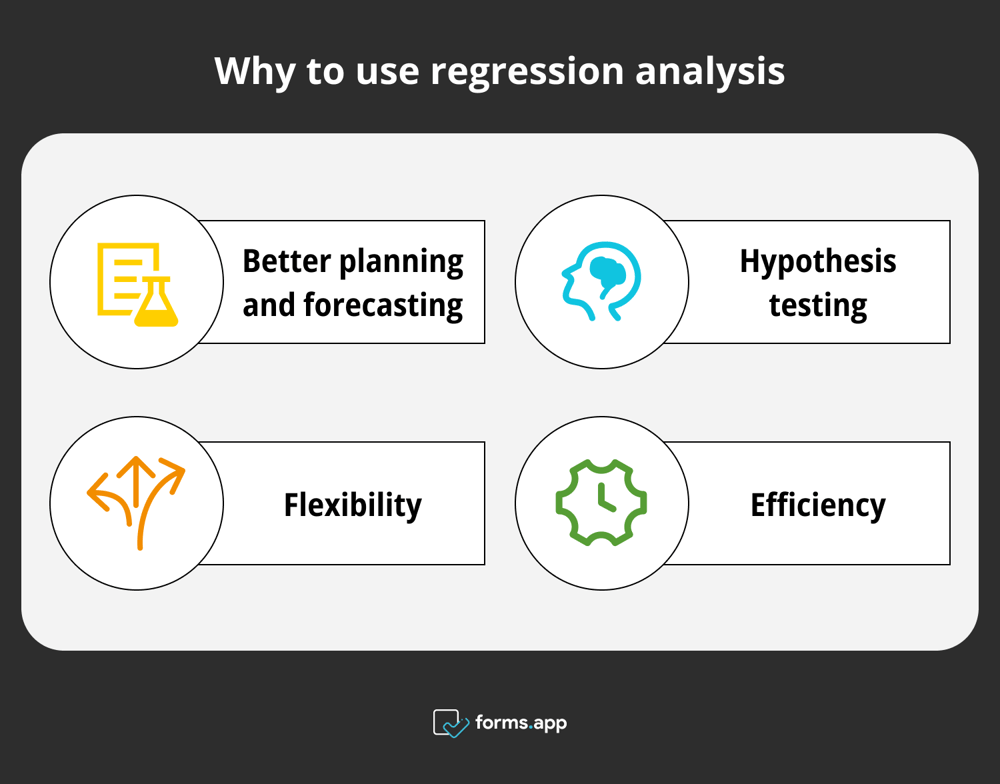
Comme mentionné, l'analyse de régression mesure l'influence des variables indépendantes sur les variables dépendantes. Les entreprises utilisent cette analyse pour faire des prédictions commerciales sur de nombreuses questions différentes. De cette manière, vous disposerez d'un mécanisme de prise de décision plus conscient et objectif. Voici les principaux avantages pour vous donner une idée :
Avantages de l'analyse de régression
- Meilleure planification et prévision: Les modèles de régression peuvent vous montrer visuellement les tendances afin que vous puissiez disposer de meilleures données lors de la planification.
- Test d'hypothèse: Comme pour tout type d'analyse, l'analyse de régression peut être utilisée pour évaluer une hypothèse spécifique.
- Flexibilité: Avec la modélisation de régression linéaire et non linéaire, les solutions pour différents types de données et questions de recherche sont plus faciles à trouver.
- Efficacité: Elle prépare votre entreprise à des solutions plus pratiques et des méthodes plus efficaces.
Questions fréquemment posées sur l'analyse de régression
Bienvenue dans la FAQ sur l'analyse de régression ! Vous pouvez vérifier ici pour obtenir plus d'informations sur ce sujet ou pour renforcer vos connaissances.
L'analyse de régression vous renseigne sur les changements, les relations et l'ordre entre les variables. Une variable dépendante est prise comme base et l'analyse tente de donner un sens à la variable dépendante et à ses liens avec d'autres variables indépendantes.
Le domaine d'application de l'analyse de régression est vaste et peut s'adapter à de nombreuses situations. Les entreprises l'utilisent, en particulier dans les études de marché, pour comprendre les attitudes des clients et développer des stratégies de marché. En outre, les entreprises l'utilisent pour examiner et calculer leur situation financière, leurs actions, l'inflation ou les taux d'intérêt.
Elle est particulièrement utile pour essayer de comprendre les tendances et les situations économiques futures à l'aide de données historiques. En outre, on la trouve également dans la phase opérationnelle, les études de terrain, les études sociales, les secteurs de la santé et du sport.
Naturellement, vous le faites d'abord lorsque vous voulez analyser des données et découvrir des modèles. Vous le faites pour prédire une situation et découvrir des possibilités. Vous le faites pour évaluer un modèle de données, le tester et apprendre son utilité. Ou bien vous avez une hypothèse et vous utilisez l'analyse de régression pour la tester.
La régression et la corrélation sont deux techniques statistiques différentes. Elles examinent toutes deux les relations entre les variables, mais diffèrent l'une de l'autre en fonction de leurs objectifs. La principale différence entre la régression et la corrélation est que la régression se concentre sur la prédiction et la modélisation.
Elle examine l'action et la réaction d'une variable indépendante avec une ou plusieurs variables indépendantes. En revanche, la corrélation examine la relation linéaire des variables entre elles. Elle permet donc de faire des synthèses plus facilement et de comprendre les situations de cause à effet.
Conclusion
Pour résumer le sujet, l'analyse de régression est généralement mentionnée dans cet article pour les entreprises. Bien que les subtilités et les caractéristiques de l'analyse des données de régression ne se limitent pas à cet article, ses principales parties et sa signification statistique vous ont été montrées.
Les parties mentionnées ici sont la définition de l'analyse de régression, la régression et l'analyse de régression multiple, les autres types non linéaires et des exemples, et enfin, ses avantages. Après avoir lu cet article et compris le monde des statistiques, prédire l'avenir est un pas de plus vers vous dans le monde réel.
Contributeurs
Recherché et rédigé par
forms.app, ton créateur de formulaires gratuit
- Nombre illimité de vues
- nombre illimité de questions
- nombre illimité de notifications