Regresyon veya basit regresyon, finans dünyası ve ilgili disiplinler tarafından yaygın olarak kullanılan bir analiz yöntemidir. Yatırım mı yapacaksınız? Regresyon analizi yapın. Emtia fiyatlarını mı inceleyeceksiniz? Çözüm regresyondur. İşletmenizin mali durumunu etkileyecek kararlar alırken regresyon analizinden faydalanabilirsiniz.
Bu makalede, regresyon analizinin basit bir tanımı verilecektir. Temel analiz türleri ve bunların örnekleri listelenecektir. Bu analizi neden kullanmanız gerektiğini anlamanız için avantajları özetlenecektir. O halde daha fazla beklemeyin ve makaleyi okumaya başlayın.
Regresyon analizi nedir?
Regresyon analizi, bir veya birden fazla bağımsız değişken ile bir bağımlı değişken arasındaki bağlantıları keşfetmek için kullanılan bir araştırma yöntemidir.
Bu yöntem, bağımlı bir değişkenin etrafında meydana gelen değişiklikleri inceleyerek değerinin tahmin edilmesine yardımcı olur. Matematiksel veri olduğu için genellikle objektiftir. Uygun araçlarla veri görselleştirme ile kullanılır ve veri noktalarının eğri veya düz çizgi desenlerini ortaya çıkarır. Böylece işletmeler bu analiz yöntemini kullanarak gelecekteki durumlar hakkında ön bilgi sahibi olurlar.
Regresyon analizi türleri ve örnekleri
Veri analizi yaparken çeşitli yöntemlerden faydalanabilirsiniz. Her yöntem benzersiz hesaplamalar içerir ve farklı konular hakkında etkili bilgiler sunar.
Her zaman küme analizi ve konjoint analizi gibi farklı türde veri analiz tekniklerinden yararlanabilirsiniz. Ancak regresyon analizi her zaman istatistiksel modelleme için ilk referansınız olacaktır. Her tür için regresyon analizi örnekleri aşağıda belirtilmiştir:
Regresyon analizi türleri
1. Doğrusal regresyon analizi
Basit doğrusal regresyon, tek bir bağımsız (tahmin edici) ve bağımlı değişken arasındaki ilişkiyi modellemek için kullanılan istatistiksel bir yöntemdir. Burada doğrusal bir ilişki olduğu varsayılır. Yani, yordayıcı değişkende bir değişiklik varsa, bağımlı değişkende de orantılı bir karşılık vardır. Bu yöntemin amacı bağımlı değişken hakkında tahminlerde bulunmaktır. Ayrıca daha karmaşık regresyon modellemelerine hazırlanmak için de kullanılır.
Regresyon formülü:
Y = a + bX + ϵ
Y – Bağımlı değişken
X – Bağımsız değişken
a – Kesme noktası
b – Eğim
ϵ – Kalıntı (hata)
Örnek: Amacınıza uygun mağazayı bulmak ve mağaza fiyatlarını tahmin etmek için bir model yapmak istiyorsunuz. Belirli bir mağaza fiyatının bağımlı değişken olduğunu varsayalım. Bu X dolardır. Bağımsız değişken bina alanıdır. İki değişken arasındaki ilişkiyi analiz ediyorsunuz. En iyi uyum çizgisi ile mağaza fiyatlarını modellemede görünür ve tahmin edilebilir hale getiriebilirsiniz.
2. Çoklu regresyon analizi
Çoklu regresyon analizi, basit doğrusal regresyon modeline birden fazla değişken eklenerek gerçekleştirilir. Buradaki amaç, her bir değerin katsayısını doğrusal bir kombinasyonla bulmaktır. Farklı tahmincilerdeki eşzamanlı değişikliklerin bağımlı değişkeni nasıl etkilediğini anlamanızı sağlar.
Örnek: Bu tür analizde, yukarıdaki mağaza arayışınıza özellikler eklersiniz. Örneğin, bir kileri, bir otoparkı, bir çatı katı vb. olabilir. Mimari özellikler eklenince mağaza fiyatlarının değişip değişmediğini gözlemleyebilirsiniz.
3. Lojistik regresyon analizi
Bu yöntem doğrusal değildir ve bir veya daha fazla değişkenle meydana gelen olayların olasılığını tahmin etmek için kullanılır. Burada mantıksal bir ikili değişken kullanılır, yani evet/hayır, doğru/yanlış. Olasılıklar sigmoid eğrisi olarak bilinen bir fonksiyonla eşleştirilir. Yani, kombinasyonlar 0 ile 1 arasındaki olasılıklara dönüştürülür.
Örnek: Müşterilerinizin yeni ürününüzü tercih edip etmeyeceklerine ilişkin olasılıkları hesaplamak istiyorsunuz. Öncelikle, müşterilerinizin demografik özelliklerini ve daha önce piyasaya sürdüğünüz ürünlere yönelik tutumlarını içeren bir veri seti hazırlarsınız. Bu veriye uygun lojistik modelleme ile olası sonuçları ikili formda öğrenebilirsiniz. Ayrıca müşteri davranışlarını anlatı analizi ile daha detaylı analiz edebilirsiniz.
4. Polinom regresyon analizi
Bu, doğrusal olmayan bir ilişkideki değişkenleri modellemek için kullanılan bir regresyon tekniğidir. Daha esnek bir veri analizi sağlar. Polinom regresyon analizi, özellikle kötü performans gösteren bir model oluşturduğunuzda ve gerçek değerlerle eşleşmediğini fark ettiğinizde referans kaynağınızdır. Veri noktalarının örüntülerini takip ederek en uygun çizgiyi tahmin etmenizi sağlar.
Örnek: Bir gıda ürününün mevsimlere bağlı olarak daha fazla satılıp satılmadığını analiz etmek istiyorsunuz. Aylara ve mevsimlere göre sattığınız gıda ürünleri hakkında veri toplarsınız. Ancak doğrusal bir ilişki olmadığı aşikar. Bu nedenle polinom regresyon analizi uygulayabilirsiniz. Polinom eğrisi ile mevsimsel dalgalanmaları daha hassas şekilde tahmin edebilirsiniz. Böylece yeni pazarın stratejileri için ortam hazırlanmış olur.
Regresyon analizinin avantajları
Belirtildiği gibi regresyon analizi bağımsız değişkenlerin bağımlı değişkenler üzerindeki etkisini ölçer. İşletmeler bu analizi birçok farklı konuda iş tahminleri yapmak için kullanırlar. Bu sayede daha bilinçli ve objektif bir karar alma mekanizmasına sahip olursunuz. Aşağıda size fikir vermesi açısından başlıca avantajlar sıralanmıştır:
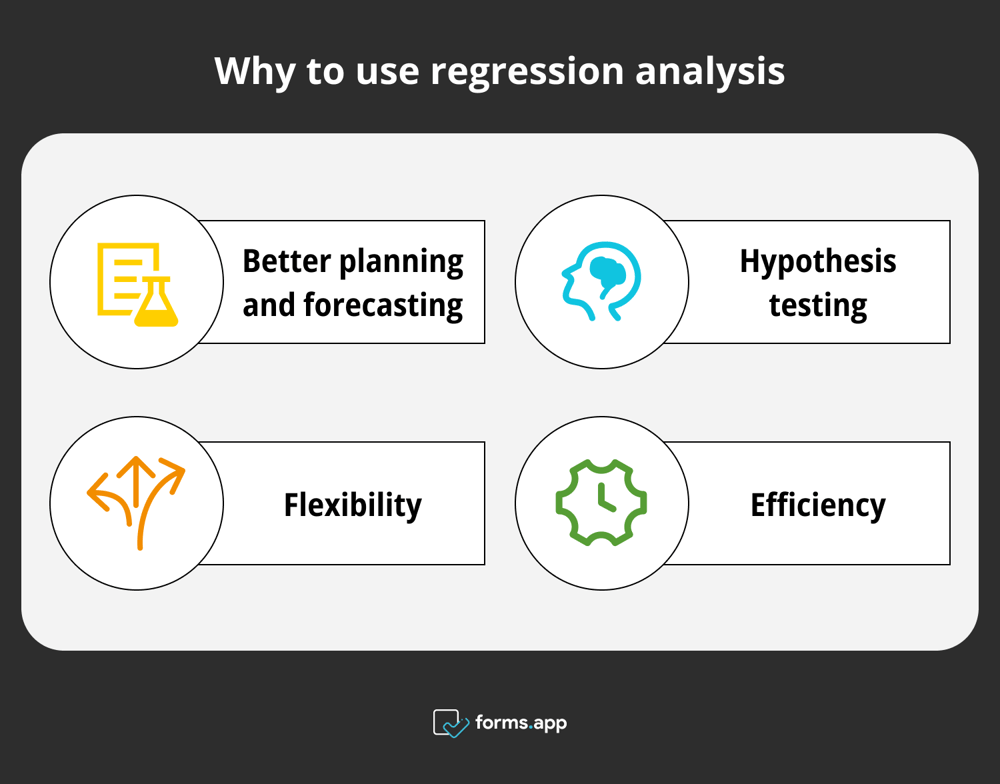
Regresyon analizinin avantajları
- Daha iyi planlama ve tahmin: Regresyon modelleri, eğilimleri görsel olarak göstererek daha iyi verilere sahip olmanızı sağlar.
- Hipotez testi: Her türlü analizde olduğu gibi regresyon analizi de belirli bir hipotezi değerlendirmek için kullanılabilir.
- Esneklik: Doğrusal ve doğrusal olmayan regresyon modelleri ile farklı veri tiplerine ve araştırma sorularına çözümler daha kolay bulunabilir.
- Verimlilik: İşletmenizi daha pratik çözümler ve etkili yöntemler için hazırlar.
Regresyon analizi hakkında sıkça sorulan sorular
Regresyon analiziyle ilgili sıkça sorulan sorular bölümüne hoş geldiniz! Bu bölümde bu konuyla ilgili daha fazla bilgi edinebilir veya bilginizi pekiştirebilirsiniz.
Regresyon analizi size değişkenler arasındaki değişimler, ilişkiler ve düzen hakkında bilgi verir. Burada bir bağımlı değişken temel alınır ve analiz bağımlı değişkeni ve onun diğer bağımsız değişkenlerle olan bağlantılarını anlamlandırmaya çalışır.
Regresyon analizinin uygulama alanı geniştir ve birçok duruma uyum sağlayabilir. İşletmeler özellikle pazar araştırmalarında, müşteri tutumlarını anlamak ve pazar stratejileri geliştirmek için regresyon analizini kullanırlar. Bunun dışında şirketler finansal durumlarını, hisselerini, enflasyonu veya faiz oranlarını incelemek ve hesaplamak için kullanırlar.
Bu yöntem, özellikle geçmiş verileri kullanarak gelecekteki eğilimleri ve ekonomik durumları anlamaya çalışırken faydalıdır. Bunların dışında operasyon aşamasında, saha çalışmalarında, sosyal çalışmalarda, sağlık ve spor sektörlerinde de ondan yararlanılır.
Verileri analiz etmek ve örüntüleri ortaya çıkarmak istediğinizde; herhangi bir durumu tahmin etmek ve olasılıkları ortaya çıkarmak için; bir veri modelini değerlendirmek, test etmek ve kullanışlılığını öğrenmek için regresyon analizi yapabilirsiniz. Bunların dışında, hipotezinizi test etmek için regresyon analizini kullanabilirsiniz.
Regresyon ve korelasyon iki farklı istatistiksel tekniktir. Her ikisi de değişkenler arasındaki ilişkileri inceler ancak amaçlarına göre birbirlerinden ayrılırlar. Regresyon ve korelasyon arasındaki temel fark, regresyonun tahmin ve modellemeye odaklanmasıdır.
Bağımsız bir değişkenin bir veya daha fazla bağımsız değişkenle etki ve tepkisini inceler. Korelasyonda ise değişkenlerin birbirleri ile olan doğrusal ilişkisi incelenir. Sonuç olarak özetlemelerin daha kolay yapılmasını ve neden-sonuç durumlarının anlaşılmasını sağlar.
Sonuç
Konuyu özetlemek gerekirse bu makalede genel olarak işletmeler için regresyon analizinden bahsedilmiştir. Regresyon veri analizinin incelikleri ve özellikleri bu makaleyle sınırlı olmamakla birlikte, temel bölümleri ve istatistiksel önemi vurgulanmıştır.
Burada bahsedilen bölümler regresyon analizinin tanımı, regresyon ve çoklu regresyon analizi, diğer doğrusal olmayan tipler ve örnekler ve son olarak da bu yöntemin faydalarıdır. Bu yazıyı okuduktan ve istatistik dünyasını anladıktan sonra, gerçek dünyada geleceği tahmin etmek size bir adım daha yakın.
Atakan tarih, sosyoloji ve psikoloji gibi çeşitli alanları araştırmayı sever. Bildiği diller arasında İngilizce ve Korece bulunmaktadır. Veri analizi, veri tipleri ve yöntemleri konularında uzmanlığı bulunmaktadır.
